Encryption algorithms

Atari used an advanced system for the encryption of cartridge headers. The entire process for the creation of a bootable cartridge header is covered in another chapter. This chapter focuses on the actual encryption of a header. The header for the Atari Lynx cartridges needed to be encrypted in similar fashion as the decryption performed by the Atari Lynx at startup. The encryption is the reverse of the decryption process and vice versa. The main purpose of the encryption is to make the header both unreadable, unchangeable and non-reproducible.

The total encryption algorithm involved two steps:

1. Obfuscation
2. Encryption

The obfuscation scrambles the header around, so it becomes less obvious to see or analyze what the actual data is. It is an additional hurdle to take when a header might get decrypted. It would not be obvious that the data was correctly decrypted, because the decrypted data does not look like 65C02 assembly yet.

The encryption itself is performed by using the RSA algorithm, which uses a set of three very large prime numbers that is nearly impossible to guess or reconstruct. Only when the exact keys are used can data be encrypted and later decrypted, provided that the same key set are used for each. This implies that it is very important to keep the keys safe.

For all that it matters an cartridge header for the Atari Lynx is simply a number of bytes containing code and data that the 65C02 can execute and use. From here on in these bytes are referred to as the unencrypted (header) data.

Obfuscation

The purpose of the obfuscation step is to prevent the decryption of the header to return the original code that is immediately executable or readable. Only after both decryption and de-obfuscation do the bytes become code and data that can be run on the processor. Therefore, the obfuscation performed when creating the header should be reversible. The de-obfuscation algorithm must be simple enough to allow it to be performed on the Atari Lynx with its small 64KB memory and limited compute power of the 65C02. Both the obfuscate and de-obfuscate algorithms are very similar in the way they work, so the obfuscation has the same complexity (or lack of it) as the de-obfuscation.

The obfuscation algorithm takes bytes from an array of arbitrary length. It subtracts the value of a byte at any position in the array from the next. The first byte is always unaltered. The result of this obfuscation is stored in reversed order before being encrypted.

The original routine was implemented in C as follows:

int i, j, checksum=0;
unsigned char array[50];

for (i=49; i>=0; i--) {
    if ( (j = getc(fpin)) < 0) { 
        printf ("Error reading input file: %s\n", argv[1]);
        exit (1);
        }
    array[i] = j-checksum;
    checksum = j;
    }

Notice how it is running from the end to the start of the array, avoiding having to store the original value of a byte before being overwritten.

As an example, take an array of bytes from an unencrypted header:

0x80, 0x00, 0x20, 0x4f, 0x02, 0x64, 0x05, 0xe6, ...

Reading right to left, the algorithm would subtract 0x05 from 0xe6 to 0xe1, and 0x64 from 0x05 wrapping to 0xa1, and so on. After performing all subtractions and reversing the order this will become an array ending in these numbers:

..., 0xe1, 0xa1, 0x62, 0xb3, 0x2f, 0x20, 0x80, 0x80

As the length of the array is not relevant for the algorithm it is possible to choose any convenient size of data to work on. The code for obfuscation shows that the size is a fixed 50 bytes. The reason will become evident in a moment.

RSA Encryption

The encryption step involves actual RSA encryption. At the time this was a very advanced and strong encryption mechanism, even though the chosen key length might not be considered secure in present days. It was more than good enough in the ’90s to protect the header of Atari Lynx cartridges from tampering or inspection.

Interesting fact

By comparison the Sega Game Gear and Nintendo Gameboy cartridges only had a specific layout in their header without any encryption. The layout was not fixed and any checks performed were done on plain bytes. Anyone was able to both read and change values in the cartridge and also header.

RSA encryption is an asymmetric encryption algorithm. The algorithm is applied to data that needs protecting. Once encrypted the data cannot be read anymore and decryption is only possible when in possession of the correct key.

RSA uses a public and private key, each consisting of an exponent and modulus. The exponents are also public and private, whereas the modulus is shared and the same in both keys. All numbers involved are prime numbers and are taken to be of a certain length when expressed as individual bytes. Typical modern day key lengths are 2048 to 4096 bits. The larger the number of bits in the keys the more compute power is required to calculate the encrypted version of data or the decryption afterwards. The Atari Lynx used a key length of 408 bits (which is 51 bytes).

The public and private keys are so named for a reason. The public key can be freely shared to anyone, but the private key must always be safeguarded and protected from being exposed. Only the owner should be in posession of the private key.

The asymmetric nature of the algorithm give two types of application on data:

1. Encryption by anyone, decryption by owner
   Allows safe exchange of sensitive data to a known owner. The data is encrypted with the public key and send to the owner of the private key. Only the owner can decrypt the data and see its original content.
2. Encryption by owner, decryption by anyone
   The data is encrypted by the owner of the private key. It is transmitted to a recipient, who can decrypt it with the public key. The data is not so much safe, as anyone can decrypt it, but free from any tampering and known to have been encrypted by a known user.

The second application is the basis for the use case of the Lynx header and cartridge protection. The header is encrypted by Atari, who are the owners of the private key. That allowed Atari to encrypt and thereby protect the header from tampering and make inspection more difficult. This implies that the public key (the public exponent and accompanying modulus) were shared to the outside world. They are indeed, because the Mikey ROM has it embedded. This is certainly not a problem, as the public key is intended to be used and shared this way.

Primer on RSA mathemetics

The calculations in RSA are small and simple, yet complex to perform, as they involve very large numbers. The RSA algorithm works with exponents and a modulus of large prime numbers. The plain or encrypted data is also considered a large number (but not necessarily a prime).

The encryption of unecrypted data in the form of a number plain performed using a private key privatekey and modulus modulus is performed as follows:

$encrypted = plain^{privatekey} \mod modulus$

The block must be raised to the power of the private key and modulo divided by the modulus.

Consider the following public/private keypair with only a 12 bit key length:

Public key:
- Modulus: 3737
- Exponent: 23

Private key:
- Modulus: 3737
- Exponent: 3287

Let’s encrypt the following “data” of 1337.

$ encrypted = 1337^{3287} \mod 3737 = 483 $

The encrypted message is 483. Although just numbers do not really make that much practical sense, it can be used to reflect messages as data consisting of bytes that represent characters or code.

The value of $1337^{3287}$ is extermely large 3,92586779e+10275 with well over 10.000 digits to represent it as a decimal integer, or 4267 bytes. The number of bytes required for the maximum achievable size would be around 6143 bytes for a 12 bit key length. Imagine what a 2048 bit long key would render as intermediate results.

The decryption of data is similar to encrypting it. This time the public exponent is used to raise the encrypted value to the power, so it is:

$plain = encrypt^{publickey} \mod modulus$

For our example the encrypted message of 483 becomes the following when decrypted:

$ plain = 483^{23} \mod 3737 = 1337 $

The original message is returned by decryption as expected.

Both formulas use a modulo division where only the remainder after division is taken. It implies that the result can never be larger than the value of the modulus. Typically, RSA encryption can only encrypt blocks of data that are less than the key length being used. Larger data needs to be divided into separate block that are within the allowed length. Encryption is performed on a block-by-block basis.

Atari Lynx encryption keys

The Lynx encryption keys were chosen to be 51 bytes long each. This was within the practical limits of calculations and also for practical purposes that will become evident shortly. In effect, the Lynx encryption keys can be used to encrypt binary data of at most 50 bytes, one byte less than the modulus as discussed above. The last byte cannot exceed the most important byte value of the modulus 0x35, rendering the 51st byte useless for decryption.

The public keypair consists of the modulus and the public exponent. It is common to choose one of the prime numbers 3, 5, 17 or 63367. The reason is that public keys are exposed, as well as the modulus. Since the decryption raises the encrypted data to the power of the public key, it might as well be a small prime number to make the calculations easier and faster. Atari chose the smallest prime number 3.

When the prime number 3 is expressed as a 51 byte number it looks like this:

public exponent:
000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000003

The modulus, which is part of both the public and private key, is available both to Atari and to everyone with an Atari Lynx. The console needs to know the modulus to be able to perform decryption. The next prime number is the modulus accompanying the public exponent.

modulus:
35B5A3942806D8A22695D771B23CFD561C4A19B6A3B02600365A306E3C4D63381BD41C136489364CF2BA2A58F4FEE1FDAC7E79

The bytes for the modulus are inside Mikey’s ROM at the offset of 0x19a to 0x1cc from the start of the ROM at $FE00.

This puts the modulus at $FF9A to $FFCC as absolute address.

Atari’s private key for Atari Lynx

Atari meant to keep the private exponent secret and store it securely. Atari devised a way to not have a single file containing the key, as it would be too easy to loose track of the one file or any media containing it.

Originally Atari had three separate encryption disks containing one “keyfile” each, keyfile.1, keyfile.2 and keyfile.3. None of these files contained the private exponent by itself. Only when the three keyfiles are combined can the private exponent be generated. Each keyfile was already 51 byte long, so there was more involved than simply adding three part together sequentially.

During the encryption process the private key would be built in-memory by loading all three disks consequtively. The keyfiles contain the hexadecimal representations of a 51-byte long array of bytes. Here are the contents of each of the three files:

Keyfile 1:
ea6cadb2abb1d3ee856fd336c0c1161d3144651a2281b5b826ddce0f8fbb25c81d34031fb4b9aedacfde75c1d2ed354bcc1158
Keyfile 2:
14d63008355728ef2ba325b7118c622d167a7dee57e73718c996e5a963496815f66c128c9eebdaefbd753a9e7d02e6e9fdd797
Keyfile 3:
dd74f0b7eee26b6db775ccca1d65dcd435e209d018469bf596cc80fa44eaee0e23bb36fe6822bfb5537df2fb86829413d4246c

The three keys need to be XOR‘ed together to make the final private encryption key.

private exponent:
keyfile1 ^ keyfile2 ^ keyfile3 = 
23ce6d0d7004906c19b93a4bcc28a8e412dc11246d2019557987ab5ca818a3d3c8e3276d4270cb8021d6bda4296d47b1e5e2a3

The complete RSA encryption public/private keypair is composed of the public and private exponents and the modulus.

private key: 
23ce6d0d7004906c19b93a4bcc28a8e412dc11246d2019557987ab5ca818a3d3c8e3276d4270cb8021d6bda4296d47b1e5e2a3
public key:
000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000003
modulus:
35b5a3942806d8a22695d771b23cfd561c4a19b6a3b02600365a306e3c4d63381bd41c136489364cf2ba2a58f4fee1fdac7e79

Fact

This public exponent prime number 3 will not be found anywhere, but implicitly as a double multiplication during the decryption process:
$block^3 = blockblockblock$

Performing encryption and decryption

Notice how the RSA formulas for encryption and decryption have a similar shape.

$ encrypted = plain^{privatekey} \mod modulus
plain = encrypt^{publickey} \mod modulus $

Both of these have a power and a modulo division. In modern programming languages it is fairly trivial to perform the RSA calculations, as there are many libraries available for exactly this formula.

For example, the System.Numerics namespace in .NET offers the BigInteger class that can do this exact calculation with the static ModPow method. The following piece of C# code demonstrates the use.

using System.Numerics;
BigInteger data = new BigInteger(block);
BigInteger plain = BigInteger.ModPow(data, privateExponent, modulus);

It assumes that privateExponent and modulus are two variables of type BigInteger that are already instantiated with the respective byte arrays of the private exponent and modulus for the private key.

Important

The order of the bytes in the array representing the public and private exponent as well as the modulus is dependent on the endianness of the system used. The keyfiles contain the values in the correct order for a big-endian system such as PowerPC and 68000 based computers, such as the Commodore Amiga used for Handy development.
For little-endian machines such as x86, x64 and ARM processors, the arrays of bytes for the keys and modulus need to be reversed. The unencrypted and encrypted data are normal arrays of the data blocks.

Big-endian: 23 ce 6d 0d ... b1 e5 e2 a3
Little-endian: a3 e2 e5 b1 ... 0d 6d ce 23

The order of importance in the array is on a byte by byte basis. The order of the bits inside a byte are unaffected.

Blocks and frames

Remember how the encryption keys are 51 bytes long, implying that it can only be used on pieces of data of at most 50 bytes. However, the code and data of the boot loaders typically exceeds that size, so the overall process must split the loader into blocks of data that fit within the limits of the encryption algorithm.

The obfuscation algorithm works on data of any size, so exactly 50 bytes will work just fine. It will always use exactly 50 bytes, so any block of data that has less bytes should be filled with zeros. Not quite surprisingly the raw boot loader files are usually 150 and 250 each, both multiples of 50.

Since the blocks are only 50 bytes long and the encryption requires numbers of 51 bytes a non-zero byte 0x15 is added at the beginning of the byte array representation for the large integer (meaning the most significant byte of the number). The data is now 51 bytes long, but neatly stays within the boundaries of the modulus because its most significant byte 0x15 is less than that of the modulus 0x35. As a consequence, you can recognize an obfuscated binary block by its first byte, which will always be 0x15.

The next step is to iterate through each of the obfuscated blocks and encrypt these one by one.

The blocks are put together to form an encrypted frame. The number of blocks inside of the frame are expressed by a block indicator. The indicator is calculated by subtracting the number of blocks from 256 (or 0x100). A three block frame has a block indicator of 0x100 - 0x03 = 0xFD. The block count preceeds the raw data of the encrypted blocks.

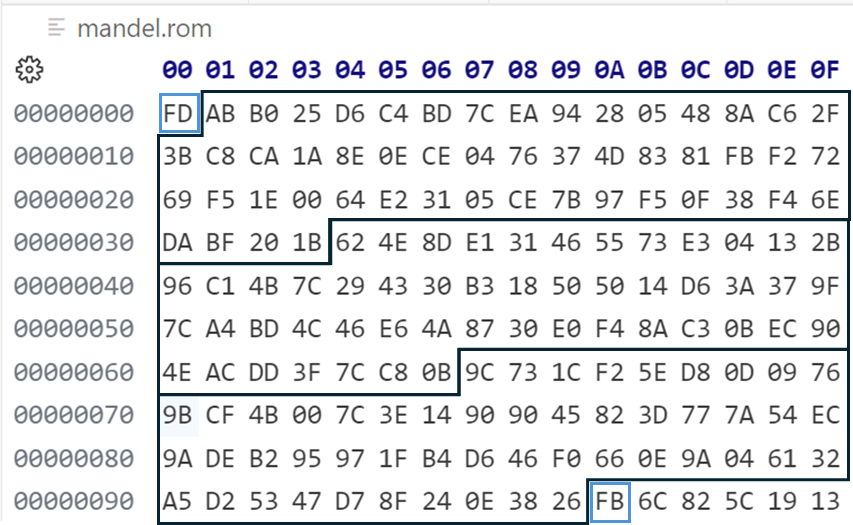
Complete example: micro bootloader

The micro bootloader has a minimalistic 48 byte first stage that fits well within the size of a single block. The code of the loader is discussed in the chapter on boot loaders. The compiled byte array serves as example data to perform a full encryption process.

Here is the compiled assembler source code padded with two 0x00 bytes at the end to create a size of 50 bytes:

9c f9 ff a0 1f a9 00 99 a0 fd 88 10 fa a9 04 8d
8c fd a9 1a 8d 8a fd a9 0b 85 1a 8d 8b fd a2 00
a0 97 ad b2 fc 9d 68 fb e8 88 d0 f6 4c 68 fb 00 
00 00

The obfuscation algorithm changes this into the following array:

9c 5d 06 a1 7f 8a 57 99 07 5d 8b 88 ea af 5b 89
ff 71 ac 71 73 fd 73 ac 62 7a 95 73 fe 72 a5 5e
a0 f7 16 05 4a a1 cb 93 ed a0 48 26 56 1c 93 05
00 00

Notice how the first byte is unaltered and all other bytes have changed into different values (except the last two bytes).

Before being encrypted the bytes are reversed in order and preceded by the special 0x15 marker byte.

15 00 00 05 93 1c 56 26 48 a0 ed 93 cb a1 4a 05
16 f7 a0 5e a5 72 fe 73 95 7a 62 ac 73 fd 73 71
ac 71 ff 89 5b af ea 88 8b 5d 07 99 57 8a 7f a1 
06 5d 9c

The obfuscated data is now 51 bytes long and ready to be encrypted. After encryption using the private key the result is the following byte array:

b6 bb 82 d5 9f 48 cf 23 37 8e 07 38 f5 b6 30 d6
2f 12 29 9f 43 5b 2e f5 66 5c db 93 1a 78 55 5e
c9 0d 72 1b e9 d8 4d 2f e4 95 c0 4f 7f 1b 66 8b
a7 fc 21

This encrypted frame consists of 1 block, so the full encrypted loader indicates this with a leading block count of $100 minus 1 is 0xff.

ff b6 bb 82 d5 9f 48 cf 23 37 8e 07 38 f5 b6 30
d6 2f 12 29 9f 43 5b 2e f5 66 5c db 93 1a 78 55
5e c9 0d 72 1b e9 d8 4d 2f e4 95 c0 4f 7f 1b 66
8b a7 fc 21

This header can be found in most cc65 compiled Lynx programs, unless one has explicitly chosen for an original or other custom header with a different boot loader.

Conclusion

The encryption process for Atari Lynx cartridge headers was relatively advanced at the time. It required tooling not found in the Handy development kit, but private to Atari. Nowadays it is fairly trivial to encrypt and decrypt headers, consisting of frames with blocks, using modern tool chains. The chapter on headers explains how they are created using the original tooling as well as with modern mechanisms.

Reference materials

• Handy encryption tooling and source code:
  https://github.com/atarilynx/handy-encryption